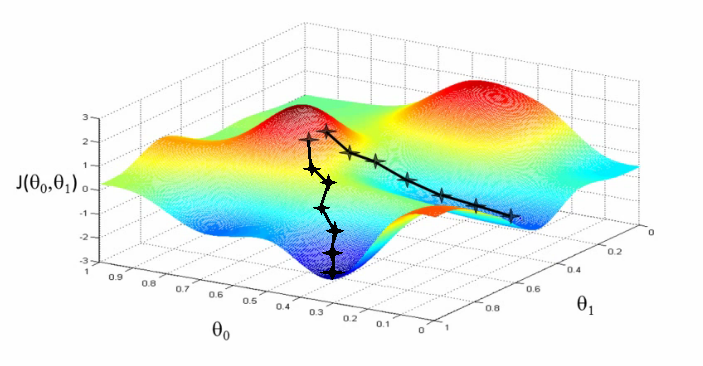
Here we will calculate the heuristic function, which is basically an approximation of output value.
And the output value is a multi-variable linear function of x.
For example f(x) can be
Below is the tested code for Gradient Descent Algorithm. I have designed this code based on Andrew Ng's Notes and lecture. This code follows linear regression model of iterating till convergence is achieved. The code here tries to minimize the error by iteratively updating the coefficient of the equation
In each iteration, We need to perform 3 operations.
The heuristic function is an approximation of the output value. The closer it is to the output value(y) the better it is.
The difference between the heuristic and the actual value is the error value. Our aim is to minimize this error.
Using the actual value, heuristic and learning rate we adjust all the values of the coefficient of variables.
Repeat these 3 steps till convergence is achieved.
while (J(y, h) > 0.1){
for (int i = 1; i < y.length; i++) {
//1. calculate heuristic
h[i] = c[0];
for (int j = 1; j < c.length; j++) {
h[i] += c[j] * x[i][j-1];
}
//2. Calculate Error
double delta = (y[i] - h[i]);
//3. update constants
c[0] += a * delta;
for (int j = 1; j < c.length; j++) {
//update cj for xj
c[j] += a * delta * x[i][j-1];
}
}
}The learning rate (α) needs to be small. Here we are taking it 10-6. Since we have a smaller dataset. You can take it between 0.1 to 0.01 if you have a large dataset otherwise, it will take a lot to converge. If it's larger than this value, it reaches the bottom and misses and starts moving up again. If its smaller than this value, it tends to never converge.
Now, let's talk about convergence. We want the δ value to become 0 for each dataset. So we try to minimize the sum of squares of errors
Convergence will be achieved when J(θ) is very small or zero.
@Field def prevSum=0
//convergence test is true if the error is less than 0.1
def J(y, h){
double sum = 0.0
//why we are minimizing the sum of squares
for(i=0; i<y.length; i++){ //for each training set
sum += (y[i] - h[i])**2
}
sum = sum/2
//negligible difference between errors in two consecutive iterations
//assign the error to be minimized to 0
if((prevSum - sum).abs() < 10**-10) sum = 0;
prevSum = sum //for taking difference in iteration
//converge if error
return sum
}If J(θ) does not change over iterations, we must stop the iterations. That means the solution is not going to go further down.
The below performs supervised learning on a given test.csv file. You can change the code to add more features. I haved added 2 features.
import groovy.transform.Field
/**
* Given x values of training set and corresponding y values
*/
def stochastic(xlist, ylist) {
x = xlist
y = ylist
def a = 0.000001; //value of alpha
def h = new double[y.length]; //heuristics same as y
def c = new double[x[0].length + 1]; //constants initliazed as 0.0
while (J(y, h) > 0.1){
for (int i = 1; i < y.length; i++) {
//1. calculate heuristic
h[i] = c[0];
for (int j = 1; j < c.length; j++) {
h[i] += c[j] * x[i][j-1];
}
//2. Calculate Error
double delta = (y[i] - h[i]);
//3. update constants
c[0] += a * delta;
for (int j = 1; j < c.length; j++) {
//update cj for xj
c[j] += a * delta * x[i][j-1];
}
}
}
printCoefficients(c)
}
@Field def prevSum=0
//convergence test is true if the error is less than 0.1
def J(y, h){
// println h
double sum = 0.0
//why we are minimizing the sum of squares
for(i=0; i<y.length; i++){ //for each training set
sum += (y[i] - h[i])**2
}
sum = sum/2
//negligible difference between errors in two consecutive iterations
//assign the error to be minized to 0
if((prevSum - sum).abs() < 10**-10) sum = 0;
prevSum = sum //for taking difference in iteration
println sum
//converge if error
return sum < 0.1
}
def printCoefficients(c){
print("y = ${c[0].round(2)}")
for (int j = 1; j < c.length; j++) {
print(" + ${c[j].round(2)}*x${j}");
}
}
def x = new double[201][2];
def y = new double[201];
int i=0;
new File("data.csv").eachLine{ line ->
def tokens = line.split(",")
if(tokens[0]?.trim()){
x[i][0] = tokens[0] as double
x[i][1] = tokens[1] as double
y[i] = tokens[2] as double
assert 2*x[i][0] + x[i][1] + 18 == y[i]
i++
}
}
stochastic(x, y);